|
§ 5 Ingewikkeld optellen: het additietheorema
Naar Uitleg §6 Maxwell
Naar Uitleg
§5 Plus
Naar Uitleg §4 Effect op lengte en
tijd
Naar Uitleg Inhoud
Naar
Vertaling §5 Additie theorema
Naar Centrale Hal
Wat moeten we doen als zich in het stelsel-in-beweging een bewegend voorwerp
bevindt? Welke snelheid heeft dat voorwerp als je het waarneemt vanuit het
stelsel-in-rust? Die vraag stelde Einstein zich. Het probleem er achter is dat
als het stelsel–in–beweging bijna de lichtsnelheid heeft en het voorwerp
heeft ook bijna de lichtsnelheid dan zou je denken dat het voorwerp ten opzichte
van het stelsel–in–rust bijna tweemaal de lichtsnelheid heeft. Dat kan niet!
De lichtsnelheid is immers de hoogste snelheid. Wij storten ons op dat probleem.
We zullen ontdekken dat 2 plus 2 niet gelijk is aan 4.
We stellen ons voor dat in het stelsel-in-beweging een voorwerp met een
constante snelheid in het ξ–η – vlak
beweegt. Niet langs de ξ–as
van het stelsel-in-beweging, maar in een willekeurige andere richting. We kiezen
de assen van het stelsel-in-rust uiteraard zodanig dat het ξ–η–vlak
en het x–y–vlak samenvallen, zodat het voorwerp tevens in het x–y–
vlak beweegt. Het x–y–vlak en het ξ–η–vlak
schuiven langs elkaar met een onderlinge snelheid v (zie figuur 501).
De snelheid van het voorwerp in het x–y–vlak zullen we vinden door
consequent de transformatieformules toe te passen.
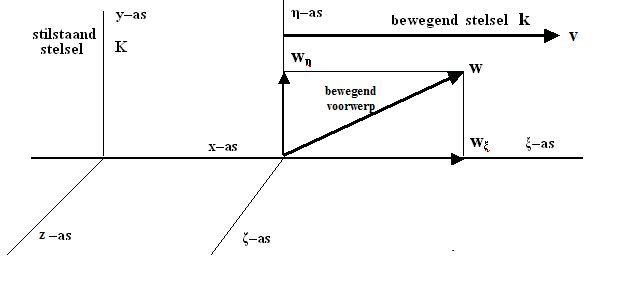
Figuur 501 Het voorwerp beweegt ten opzichte van het stelsel-in-beweging
Het voorwerp beweegt met een constante snelheid en richting w in het
stelsel-in-beweging en de plaats die het voorwerp na τ
seconde heeft bereikt (als we de oorsprong zo hebben gekozen dat op τ
= 0 het voorwerp door de oorsprong bewoog), is te beschrijven met:
ξ = wξ . τ
η = wη . τ
ζ = 0
Hierin is wξ de
snelheidscomponent langs de ξ–as
en wη de
snelheidscomponent langs de η–as.
Het voorwerp beweegt in het ξ– η –
vlak en blijft in dat vlak. Zijn ζ
– coördinaat is nul en blijft nul. Na een tijd τ
heeft het voorwerp een afstand in het vlak afgelegd, waarvan we de component in
de ξ – richting en de
component in de η – richting
kunnen berekenen met de formules hierboven.
Hoe beweegt het voorwerp zich nu volgens de waarnemers in het
stelsel-in-rust?
Het antwoord op deze vraag vinden we door de transformatieformules in te
vullen.
Hier zijn ze nog een keer:
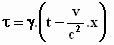
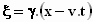 η = y
ζ = z
η = y
ζ = z
Vul de uitdrukkingen voor ξ
en τ in in de vergelijking ξ
= wξ . τ
voor de beweging in de ξ –
richting. Je krijgt:
γ . (x – v . t) = wξ
. γ . ( t – 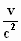 .
x) .
x)
De factor γ kan worden
weggestreept. Des te beter! Doe dat.
Herschik de vergelijking zo dat termen met een x er in links van het
=teken komen te staan en die met een t er in rechts. Dit wordt het
resultaat:
x + wξ . 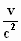 .
x = wξ . t + v . t .
x = wξ . t + v . t
Breng x en t buiten haakjes:
x . ( 1 + wξ . 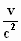 )
= (wξ + v) . t )
= (wξ + v) . t
Voor de beweging langs de x–as in het stelsel-in-rust heb je nu de
uitkomst:
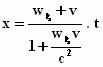
Merk op: de plaats x is gewoon evenredig met de tijd t. De
ingewikkelde term vóór t is echter niet gewoon de som van de snelheden
in de x–richting.
Op gelijke wijze pak je de formule aan voor de beweging in de η–richting:
η = wη . τ
.
Eerst vul je de uitdrukkingen voor η
en τ in:
y = wη . γ
. ( t – 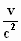 .
x) .
x)
Een vreemde eend in de bijt is de x, want je was met de y–richting
bezig. Die werk je er daarom snel uit door gebruik te maken van de formule voor x
die je net hebt afgeleid. Dat is slim!
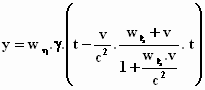
Wat je krijgt, maakt echter niet vrolijk: wat een wilde formule! Dat ga je
fatsoeneren. Pak alleen de term tussen haken aan! In stapjes:
Stap 1: De t buiten de haken halen en van de tweede term de
tellers respectievelijk de noemers met elkaar vermenigvuldigen:
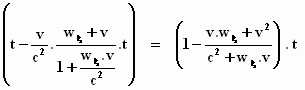
Stap 2: Het getal één anders schrijven door ‘m dezelfde noemer te
geven:
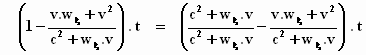
Stap 3: De termen met dezelfde noemer optellen:
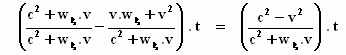
Stap 4: De teller en de noemer door c2 delen:
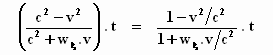
Stap 5: Gebruikmaken van γ2
= 1/(1-v2/c2):
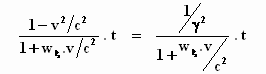
Hiermee wordt y:
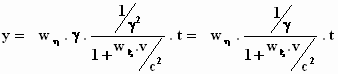 of:
of:
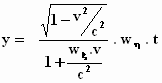
met als eindresultaat:
Ziet dit er nou zoveel beter uit? Nou, eh…..ja, iets.
Merk op: de plaats y in de y–richting is (net als x in
de x–richting) eenvoudigweg evenredig met de tijd t , maar de
snelheid is op wel zeer ingewikkelde wijze afhankelijk van v , wη
en wξ. Daar is verder
weinig aan te doen.
Voor de derde coördinaat: ζ = 0
kan simpelweg worden geschreven z = 0 . Er is geen beweging in de ζ–
of z–richting. Was het maar altijd zo eenvoudig.
Even op een rijtje gezet:
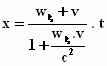
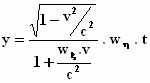 z = 0 .
z = 0 .
Je ziet hier de afgelegde afstanden in de x – , y – en z – richting.
Bedenk dat de afstand gelijk is aan de snelheid maal de tijd. De snelheden in de
x – richting en de y – richting in het stelsel-in-rust zijn
dus die ingewikkelde termen waarmee de tijd t wordt vermenigvuldigd. Als w
en v constante snelheden zijn, dan zijn die ingewikkelde termen ook
constant en dan neem je toch in het stelsel-in-rust een éénparige rechtlijnige
beweging waar.
De noemer speelt in beide uitdrukkingen een belangrijke rol. Als v en wξ
dezelfde richting hebben, is de noemer groter dan één, bij een tegengestelde
richting is hij kleiner dan één. De noemer heeft de neiging om de somsnelheid
in te tomen als de snelheden gelijk gericht zijn en de somsnelheid wat extra’s
te geven als de snelheden tegengesteld gericht zijn.
In de y–richting wordt de snelheid bovendien ingeperkt door de
wortelterm 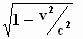 .
.
Voorbeeld: Als de cowboys op de balk passeren met een snelheid van 6/8 van de
lichtsnelheid en ze werpen met een snelheid van 1/8 van de lichtsnelheid een
lasso recht vooruit (om een koe te vangen) dan constateren wij dat de lasso met
minder dan 7/8 van de lichtsnelheid beweegt. Als ze de lasso met dezelfde
snelheid in de richting werpen waar ze vandaan komen, zullen wij constateren dat
de snelheid van de lasso groter is dan 5/8 van de lichtsnelheid.
Als ze met een uitbundig gebaar hun cowboyhoed recht omhoog werpen met een
snelheid van 1/8 van de lichtsnelheid dan zullen wij voor de hoed een lagere
snelheid waarnemen.
Wat hier bijzonder aan is, is dat je de snelheden v en w niet
vectoriëel kan optellen met behulp van het gebruikelijke parallellogram (figuur
502).
Even opfrissen: dat werkte als volgt. Als een voorwerp, gezien vanuit een
stelsel-in-rust, tegelijkertijd aan twee snelheden (twee vectoren), die
gesymboliseerd worden door twee pijlen v en w, deelneemt, vindt je
de uiteindelijke snelheid U als de pijl die de diagonaal van het
parallellogram is. Dat is vectoriëel optellen.
Denk aan iemand die van de linker– naar de rechterkant loopt in een rijdende
trein, of een schip dat vaart op een stromende rivier, enzovoort. Wanneer je de
snelheden netjes op schaal tekent, kan je gewoon de lengte van U opmeten
en de zodoende grootte van U bepalen.
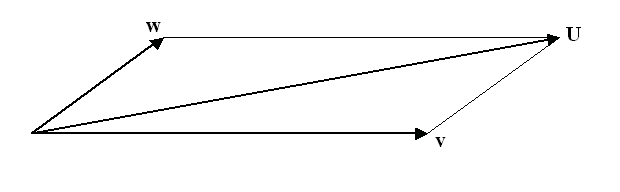
Figuur 502 Parallellogram voor het optellen van snelheden
Maar je kan er ook aan gaan rekenen. Dan is het handig om de snelheid w
in componenten te ontbinden, waarvan de ene component in de richting van v
wordt genomen en de andere er loodrecht op. Dat doen we in figuur 503. We
verkrijgen de componenten door vanuit de punt van de pijl w twee
loodlijnen neer te laten op de horizontale as respectievelijk de verticale as.
De snelheidscomponent wξ
heeft dezelfde richting als v en vergroot daarmee de snelheid in de
richting van v (en vermindert die snelheid als wξ
naar links gericht zou staan). De verticale component wη
draagt bij, noch vermindert de snelheid in de richting van v , maar voegt
een snelheid wη toe
in een richting loodrecht op de snelheid v.
 | Dat is de snelheid waarmee een schip of een vliegtuig
afdrijft van de richting waarin de voorpunt wijst. |
Met wξ , wη
en w kan een driehoek worden gevormd met w als schuine zijde en wξ
en wη als
rechthoekszijden. Volgens de stelling van Pythagoras geldt voor de zijden van de
driehoek:
w2 = wξ2
+ wη2 .
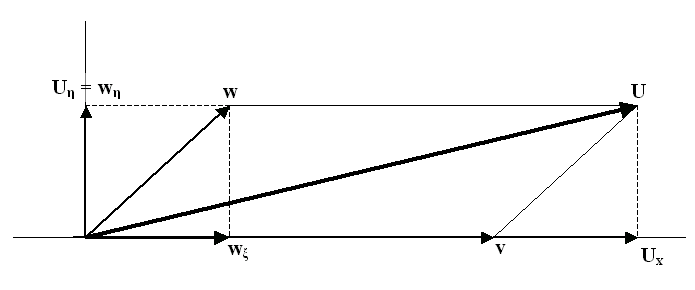
Figuur 503 Het ontbinden in componenten
Wanneer we nu naar de vectorsom U kijken, dan heeft deze twee
componenten:
Ux = wξ
+ v , de horizontale component van U, en
Uy = wη
, de verticale component van U .
Ook hier geldt Pythagoras: U2 = Ux2 + Uy2
= (wξ + v)2 + wη2.
De snelheid U van een vliegtuig dat een snelheid v door de
lucht heeft, waarbij de lucht zelf met een snelheid w in één of andere
richting stroomt, ten opzichte van de grondstations wordt dus verkregen met de
gebruikelijke manier van vectoriëel optellen:
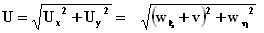 "gewone vectorsom"
"gewone vectorsom"
Terug naar de formules die Einstein had gevonden voor de verplaatsing in het
stelsel-in-rust in de x–richting en de y–richting:
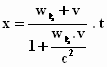 en
en 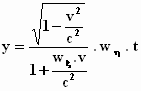
Hieruit halen we de snelheidscomponenten Ux en Uy
door te delen door t:
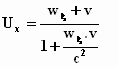 en
en 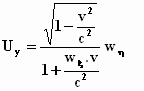
 | In de originele tekst maakt Einstein gebruik van de afgeleiden 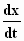 en
en 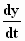 om
de snelheidscomponenten te vinden. Wij hebben hier de plaats (x of y)
gewoon gedeeld door de tijd t om de snelheidscomponenten Ux en
Uy te vinden. Dat mag omdat de termen vóór t niet afhangen
van de tijd. Ze zijn constant. om
de snelheidscomponenten te vinden. Wij hebben hier de plaats (x of y)
gewoon gedeeld door de tijd t om de snelheidscomponenten Ux en
Uy te vinden. Dat mag omdat de termen vóór t niet afhangen
van de tijd. Ze zijn constant. |
De somsnelheid U is dus te vinden uit de componenten via de stelling
van Pythagoras:
U2 = Ux2 + Uy2.
en wordt:
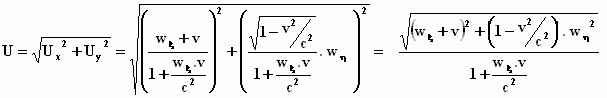
Dat ziet er knap ingewikkeld uit en het wijkt sterk af van de "gewone
vectorsom" die we eerder hadden gevonden.
Terug
De uitdrukking wordt misschien overzichtelijker als we de hoek α
er in betrekken, de richting van de beweging van het voorwerp in het
stelsel-in-beweging w ten opzichte van de ξ
– as.
Einstein heeft het voor ons uitgezocht. Het levert een wat andere
schrijfwijze op waaraan hij laat zien dat v en w symmetrisch in de
formule voor de vectorsom U zijn opgenomen. Daarmee is gezegd dat beide
snelheden dezelfde rol in de formule spelen; voor het resultaat maakt het niet
uit of de snelheid v gelijk is aan 100.000 km/s en de snelheid w
gelijk aan 140 km/s of dat v gelijk is aan 140 km/s en w gelijk
aan 100.000 km/s. Meer doen we er niet mee. Goed voor het archief. Einstein
kiest vervolgens voor een beweging met α =
0, waarmee dit uitstapje overbodig lijkt.
We zullen zijn berekening volgen, maar, voor de luiaards onder ons: ga
verder bij >>>►►►►
Nu komen we ineens in de goniometrie terecht. Wat zijn ook alweer de sinus,
de cosinus en de tangens? Even kort herhalen:
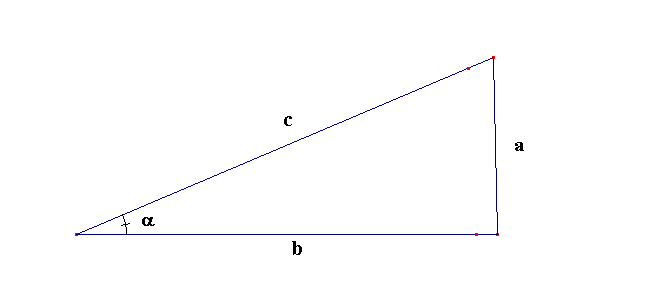
Figuur 504 Sinus, cosinus en tangens
In een rechthoekige driehoek (zie figuur 504) kan je bij de hoek α
de sinus van α aanwijzen als de
verhouding van de zijden: a/c. Voor de cosinus van α
vind je b/c en voor de tangens van α
neem je a/b. Kort genoteerd:
sin α = a/c en dus a =
c . sin α
cos α = b/c en dus b = c
. cos α
tg α = a/b en dus a = b .
tg α
Omdat in een rechthoekige driehoek de stelling van Pythagoras geldt: a2
+ b2 = c2 , volgt daaruit de belangrijke
goniometrische formule sin2α +
cos2α = 1.
In figuur 505 is de snelheid w van het voorwerp in het
stelsel-in-beweging aangegeven. De snelheid w maakt een hoek α
met de ξ–as. Met de definities
voor de sinus en de cosinus kunnen we nu voor de componenten van w
schrijven:
wξ = w . cos α
en wη
= w . sin α
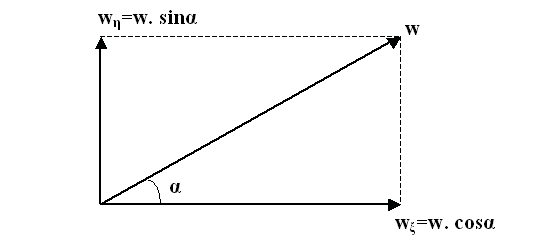
Figuur 505 De componenten van w
De hoek α is te vinden met de
sinus, de cosinus of de tangens, dat maakt niet uit. Omdat we ons richten op de
componenten van de snelheid w gebruiken we de tangens: de hoek α
is te vinden met: tg α = 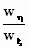 . .
Dit wordt geschreven als de hoek (arc) die bij die waarde van de
tangens hoort:
α = arctg 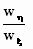 . .
 | Hier vinden we een slordigheidje in de originele tekst. Een kleine
aanwijzing dat Einstein er met zijn gedachten soms niet helemaal bij was,
maar in plaats van 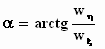 staat
er staat
er 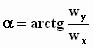 .
Slordig omdat de hoek α echt betrekking
heeft op de richting van het bewegende voorwerp in het
stelsel-in-beweging. Op het resultaat heeft het verder geen enkele
invloed, typisch Einstein! .
Slordig omdat de hoek α echt betrekking
heeft op de richting van het bewegende voorwerp in het
stelsel-in-beweging. Op het resultaat heeft het verder geen enkele
invloed, typisch Einstein! |
Vervang in de uitdrukking 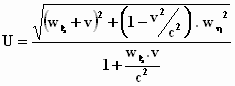 de wξ en de wη
door w . cosα en door w . sinα
. Je krijgt de uitdrukking:
de wξ en de wη
door w . cosα en door w . sinα
. Je krijgt de uitdrukking:
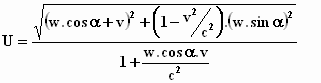
Werk dit uit tot:
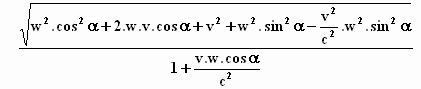
Maak nu gebruik van de bekende goniometrische formule sin2α
+ cos2α = 1 ,
dus
w2 .sin2α + w2
.cos2α = w2 ,
zodat je deze twee termen in de formule bijeen kan nemen.
>>>►►► Als je dit stukje had
overgeslagen, kan je hier weer inspringen. Je hebt niet veel gemist.
Je krijgt de uitdrukking die bovenaan blz. 906 van het origineel is te
vinden:
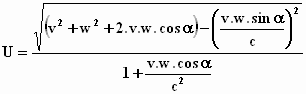 "goniometrische uitdrukking"
"goniometrische uitdrukking"
Deze schrijfwijze laat zien dat als je v verwisselt met w de
uitdrukking hetzelfde blijft. De snelheden v en w zitten
symmetrisch in de formule. Het maakt dus niet uit of het stelsel-in-beweging een
bepaalde hoge snelheid heeft en het voorwerp een minder hoge of andersom.
Tegenwoordig wordt U de "relativistische som"
genoemd.
Oefening 22
De balk met beide cowboys heeft een snelheid van 0,4 keer de lichtsnelheid.
Onder een hoek van 60° (gezien door de cowboys) schieten deze vrijbuiters in
voorwaartse richting kogels af met een snelheid van 0,6 keer de lichtsnelheid.
Bereken de componenten in het stelsel-in-beweging w ξ
en wη
.
Bereken de componenten in het stelsel-in-rust Ux en Uy
.
Bereken de "relativistische som" U
Als we het ons eenvoudig maken, nemen we α
= 0. Dan heeft sinα de
waarde 0 en cosα de
waarde 1. Het voorwerp beweegt in het stelsel-in-beweging in de positieve
ξ–richting. De formule voor
het optellen van twee parallelle snelheden, het "additietheorema",
wordt dan:
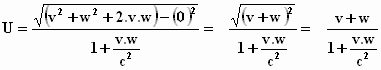
U = 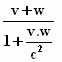 "optelformule"
"optelformule"
Hiermee wil Einstein vervolgens laten zien dat de som van twee snelheden
altijd kleiner blijft dan de lichtsnelheid. Dat is geen overbodig bewijs.
Over de snelheid van voorwerpen zijn geen aannames gedaan.
We passen de transformatieformules toe op de snelheid van gewone voorwerpen.
Zou een voorwerp sneller kunnen gaan dan het licht dat het zelf uitzendt, zoals
een vliegtuig sneller kan gaan dan het geluid dat het voortbrengt?
Dat zou wat zijn als de snelheid groter dan de lichtsnelheid zou kunnen
worden!
We kijken over de schouder van Einstein mee: Neem voor v een snelheid c
– κ en voor w een snelheid
c – λ , waarbij κ
(de Griekse letter kappa) en λ
(de Griekse letter lambda) een positieve waarde hebben en kleiner zijn
dan de lichtsnelheid.
Ingevuld in de "optelformule":
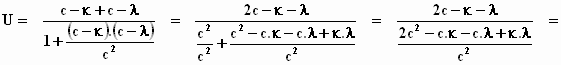
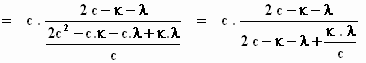
Er moet worden aangetoond dat de relativistische som van twee snelheden, die
kleiner zijn dan de lichtsnelheid, ook kleiner is dan de lichtsnelheid. Dus U
moet kleiner zijn dan c .
Dat is het geval als 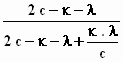 < 1
< 1
Dat is inderdaad zo, want: (2c– κ–
λ) is kleiner dan (2c– κ–
λ + κ . λ /c) omdat κ
. λ /c een positief getal is.
Dan is het quotiënt kleiner dan 1 , dus U < c.
De sommatie van twee gelijkgerichte snelheden onder de lichtsnelheid levert
weer een snelheid onder de lichtsnelheid op met dezelfde richting. Vanuit de
wiskunde bekeken, vormen de "parallelle transformaties" een
"groep". Einstein zegt het. Er wordt mee bedoeld dat alle
gelijkgerichte snelheden die kleiner zijn dan de lichtsnelheid, opgeteld in
willekeurige combinaties, altijd weer een gelijkgerichte snelheid opleveren die
beneden de lichtsnelheid is. Dat soort wiskunde gaan we maar niet op in.
Je zou je kunnen afvragen: "En als de snelheden een hoek met elkaar
maken, wat dan?"
Het is te verwachten dat twee snelheden in dezelfde richting elkaar maximaal
versterken, dus dat snelheden onder een hoek altijd een minder grote snelheid
opleveren, maar eigenlijk moet het worden aangetoond. Dat zou te ver voeren,
maar we maken het aannemelijk door het aan te tonen voor een snelheid w
die loodrecht staat op de snelheid v.
Dus met α = 90°, waarbij sinα
= 1 en cos α = 0.
Dan wordt de "goniometrische uitdrukking":
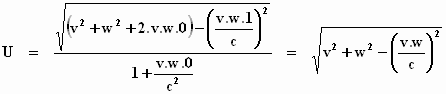
We maken hiervan:
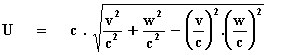
Als v = c en/of w = c wordt de uitdrukking onder het
wortelteken precies gelijk aan één. Dan is U = c. Dus als één van de
twee snelheden de lichtsnelheid is, of beide, dan is de somsnelheid ook de
lichtsnelheid en niet meer dan dat.
Als (v/c)2 en (w/c)2 kleiner zijn dan
één is de uitdrukking onder het wortelteken ook kleiner dan één. Dat is niet
zo één, twee, drie uit de formule voor U te zien. Om dit aan te tonen,
gebruiken we dezelfde methode die Einstein net hiervoor ook gebruikte. We
schrijven voor
(v/c)2 = 1 – κ
en voor (w/c)2 = 1 – λ
waarbij κ en λ
een waarde hebben tussen 0 en 1.
De uitdrukking onder het wortelteken wordt dan:
1 – κ + 1 – λ – (1 –
κ).(1 – λ) = 1 – κ + 1 – λ – 1 + κ + λ
– κ.λ = 1 – κ.λ.
Omdat het product van κ en λ
kleiner is dan 1, is 1 – κ.λ
ook kleiner dan één.
Dan geldt dus U < c .
Einstein toont vervolgens aan dat de "optelformule" in
overeenstemming is met de 2de aanname dat de snelheid van het licht
niet afhangt van de snelheid w van het voorwerp dat het licht uitzendt.
De snelheid U, van het door het met de snelheid w bewegende
voorwerp uitgezonden licht wordt namelijk, als je voor v de snelheid c
neemt:
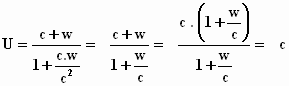
Dus U , de "som" van de lichtsnelheid en de snelheid van het
bewegende voorwerp, is weer gewoon de lichtsnelheid c !
In de laatste alinea op blz. 906 vermeldt Einstein dat de formule voor
het samenstellen van twee parallelle snelheden (die dezelfde of tegengestelde
richting hebben) gemakkelijk gevonden wordt als je de transformatieformules
toepast op een bewegend voorwerp met snelheid w langs de ξ–as
in een stelsel-in-beweging k (snelheid v ). Dat is gemakkelijk
omdat je niets te maken hebt met componenten in de η–richting.
Yes, laten we dat eens doen!
De benodigde transformatieformules zijn: 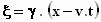 en
en 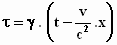
We kiezen het stelsel-in-beweging zo dat op τ
= 0 het voorwerp door de oorsprong gaat.
Ter herinnering: De transformatieformules zijn gebaseerd op de afspraak dat t
= τ = 0 als de oorsprongen van het
stelsel-in-beweging en het stelsel-in-rust samenvallen. Doe je het anders, dan
worden ze nodeloos ingewikkeld met extra constanten.
Voor de afstand die het voorwerp heeft afgelegd geldt: ξ
= w . τ
We vullen de transformatieformules in:
γ . (x – v . t ) = w . γ
. ( t –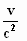 .
x ) .
x )
Gelukkig, de γ kan worden
weggestreept. Die zijn we kwijt en we houden over:
x – v . t = w . ( t – 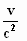 .
x ) .
x )
We brengen alles waar een x in zit naar links en alles waar een t
in zit naar rechts:
x + w . 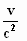 x
= w . t + v . t x
= w . t + v . t
We schikken het wat netter :
x . ( 1 + w . 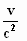 )
= ( w + v ) . t )
= ( w + v ) . t
en schrijven het zo dat de snelheid er in te zien is :
x = 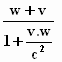 .
t .
t
Dat is hem al! De term voor de tijd t is U , de "optelformule".
Die komt nu aanmerkelijk sneller te voorschijn dan via de eerste afleiding. Er
staat tegenover dat we nu geen enkel inzicht krijgen in de afhankelijkheid van
de richting, de hoek α .
De proeven van de Fransman Fizeau (1851) en ook van de
Nederlander Martin Hoek (1868) die bedoeld waren om te onderzoeken of de
veronderstelling van Augustin Jean Fresnel (1818), namelijk dat op grond
van de golftheorie van licht de veronderstelde ether door een bewegend
object in zekere mate zou worden meegesleurd, zou kloppen, leidden tot
resultaten die door Einstein werden herkend als een directe bevestiging
van de somformule. Ruim voor de
relativiteitstheorie in zijn huidige vorm bestond, werden de eerste
formules al op tafel gelegd!
Oefening 23
Bereken de somsnelheid U voor de snelheid v = 0,6 . c en w = 0,8 . c en laat
daarmee zien dat de snelheid U kleiner blijft dan de lichtsnelheid, dus zeker
niet 1,4 . c wordt.
Het zou aardig zijn om de "somformule" aan de hand van een
plaatje met driehoeken aanschouwelijk te maken. Dat moet toch heel gemakkelijk
zijn. Een fluitje van een cent als je daarbij de driehoeken gebruikt met de
bekende verhoudingen. Met passer en liniaal willen we in een figuur ( en de
figuur mag best wat ingewikkelder zijn) een lijntje kunnen trekken dat de
somsnelheid U voorstelt.
Dat nu blijkt enorm tegen te vallen, daarom staat het resultaat van deze door
niemand gevraagde, dus mogelijk overbodige, "Spielerei" in
§5plusSomtekening.
Wie echter zelf naar de oplossing wil zoeken, verdient ontzag (oefening 24
).
Oefening 24
Ontwerp een meetkundige voorstelling voor de somformule waarbij je met behulp
van passer en liniaal de grootte van de somsnelheid weer kan geven.
Het succesvol oplossen van dit probleem kan leiden tot een "opnieuw–geboren–worden"–ervaring.
Falen leidt wellicht tot een "bijna–dood–ervaring". Succes!
Boek dicht en niet spieken!
Terug
Naar Uitleg §6 Maxwell
Naar Uitleg 5plus
|
