Foto wervelwind
Foto draaikolk
Naar Uitleg §7 Sterren
Naar Uitleg §6 Maxwell
Naar Uitleg Inhoud
Naar Centrale Hal
§ 6plus Wervelwinden en draaikolken
Het begrip rotatie wordt toegepast bij vectorvelden. Je zou het niet
denken, maar het is een hartstikke lastig begrip. We komen het in
het artikel van Einstein tegen bij magnetische en elektrische velden, maar het
is veel beter om eerst eens naar de stromingsleer te kijken waar het tenminste een
tastbaar begrip is.
In Einsteins verhaal staat bijvoorbeeld de wiskundige uitdrukking rot E
voor het elektrisch vectorveld E = (X , Y, Z).
Dat wordt uitgeschreven als:
rot E = 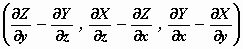
Zoals je ziet is de rotatie
van de vector E ook een vector met een x–, een y– en
een z–component. De componenten zijn opgebouwd uit partiële
afgeleiden, de 'kromme d'. We hebben ze eerder gezien ergens halverwege
de uitleg van §3. Daarbij gaat het om de verandering tengevolge van één
variabele terwijl de andere variabelen constant worden gehouden. Het bijzondere
is dat je voor de x-component van rot E de Y differentieert
naar z en Z differentieert naar y. Alles staat zo'n beetje
loodrecht op elkaar.
In de stromingsleer is het vectorveld waar het begrip rotatie op wordt
toegepast een snelheidsveld. De vector v geeft de snelheid in een zeker
punt van de vloeistof of het gas weer. Wanneer het om een horizontale stroming
gaat, heeft de snelheidsvector slechts twee componenten vx en vy.
Het is gebruikelijk om deze componenten vx en vy te
noemen in tegenstelling tot wat je verwacht naar aanleiding van het eerder
gedefinieerde coördinatenstelsel waarbij in het horizontale vlak naast de x–component
ook de z–component te vinden was en waarbij de y–component verticaal
werd getekend.
Wij geven de snelheden in het horizontale vlak dus aan met vx
en vy en de verticale richting is in dit geval de z–richting.
Als iets ronddraait, kan je meestal een as aanwijzen. Voor een draaitol is
het duidelijk. De tol (zweeptol, priktol, bromtol, gyroscoop) draait in of
schommelt om het horizontale vlak, de as staat loodrecht op het draaivlak. In
welk vlak de tol draait, is dus gemakkelijker aan te gegeven met de richting van de
draaias die er loodrecht opstaat. De draaiing kan daarom worden aangegeven met een
vector langs de draaias, die de grootte en de richting van de draaiing symboliseert. Een draaiing in het horizontale
xy- vlak geef je dus aan met een rotatievector die een bepaalde grootte en
richting langs de z–as heeft. Ook een draaikolk in het water
heeft een min of meer verticale rotatievector evenals een windhoos, een tornado (zie
fig. 1)
(of een orkaan of een stormdepressie).
Of de vectorpijl omhoog of omlaag gericht is, kan worden. bepaald met de
kurkentrekkerregel: de draaiing van je hand en de richting waarin de schroef van
de kurkentrekker zich in de kurk beweegt, horen bij elkaar. Een draaikolk, die
van boven gezien met de klok meebeweegt, heeft een rotatievector die naar
beneden is gericht, naar de negatieve z–as.
Vraag: Hebben stormdepressies op het noordelijk halfrond een opwaarts
gerichte rotatievector of een neerwaarts gerichte rotatievector?

Figuur 1 Tornado (VS.. ….. …)
De draaiing wordt dus aangegeven met een vector (grootte + richting) in de
verticale z–richting.
De rotatie van het snelheidsveld v kan nu op eenzelfde wijze als de
rotatie van het elektrische veld worden geschreven, dat wil zeggen dat de
componenten vx, vy,
vz op dezelfde plaats in de formule staan als
de componenten X, Y en Z van E:
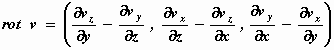
Maar, in dit geval, nu er geen snelheid in de verticale richting is, geldt vz
= 0. Maar dan is ook de afgeleide van vz naar x
of naar y gelijk aan 0: 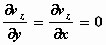
Als we verder veronderstellen dat de stroming vlak is, dat wil
zeggen dat de stroming niet afhangt van de hoogte, dan is vx
noch vy afhankelijk van z., dus
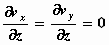 . .
Dan houden we over: 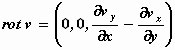 . .
De vector rot v heeft alleen een z–component. Het is een
vector met de richting van de draaias en een grootte die afhangt van hoe de
draaiing wordt gedefinieerd.
Daarmee komen we op de vraag: hoe kan je een hoeveelheid rotatie aangeven?
Vast niet in kilogrammen! Maar hoe
wel!?
Daar duiken we in!!!
Je kan je voorstellen dat je de rotatie bepaalt door aan te geven hoe krom de
stroomlijnen van het snelheidsveld ter plekke lopen. Dat zal blijken geen goed
uitgangspunt te zijn, omdat er met name cirkelvormige stromingen zijn met totaal
verschillende rotatiewaarden, afhankelijk van de snelheidsfunctie, terwijl de
kromming, langs eenzelfde cirkel, dezelfde is. Bij het begrip rotatie moet een
gebiedje rond een zeker punt erin worden betrokken.
Een tweede gedachte is de rotatie aan te geven met de snelheid waarmee het
snelheidsveld op die plaats om zijn as draait. Een nieuwe vraag doet zich voor:
"Hoe moet je dat opvatten?"
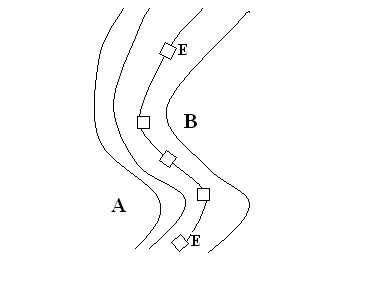
Figuur 2 Rotatie
Op de volgende manier:
Je neemt in gedachten een klein elementje E van de bewegende stof en je
bekijkt hoe het de stroming volgt. In de bochten A en B moet het
draaien (zie fig. 2). De rotatie moet worden gezien als de snelheid
waarmee dit elementje op die plek op dat moment aan het draaien is.
De vraag die hieruit voortvloeit, is: "Hoe geef je aan hoe snel iets
draait?"
In het dagelijks leven neem je daarvoor: het aantal keren per seconde dat iets
om zijn as draait. Dat is de frequentie in Hz. Maar binnen het bouwwerk van de
fysica (en de techniek) is een andere eenheid gangbaar, namelijk de
hoekverdraaiing per seconde. En deze wordt dan niet uitgedrukt in graden per
seconde, maar in radialen per seconde (rad/sec). Dit wordt de hoekfrequentie
genoemd (ook wel, maar minder helder: de cirkelfrequentie). Wanneer iets geen
cirkelbeweging uitvoert, maar wat vager om zijn as schommelt, gebruiken we het
woord hoeksnelheid. Het symbool voor hoekfrequentie, cirkelfrequentie en
hoeksnelheid is ω (in rad/s)
 |
Uitleg over radialen per seconde.
We laten in gedachten een punt P rondjes draaien langs een cirkel (zie
figuur 3). De straal van de cirkel is r. Die lengte noemen we een radius (=
Latijn voor straal) . Iedere keer als het punt langs de cirkel een afstand
heeft afgelegd die gelijk is aan r heeft het punt een radius afgelegd. De
bijbehorende hoek heet een radiaal. Omdat de omtrek van een cirkel gelijk is
aan 2 πr, zal het punt 2π
radialen hebben afgelegd bij een enkele omloop. Maar
één omloop komt ook overeen met 360º. Daaruit mag je concluderen dat 1
radiaal gelijk is aan 360º/2π
= ongeveer 57,3 º. |
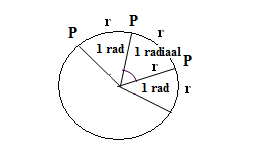
Figuur 3 De radiaal
De rotatie kan dus worden aangegeven met de hoeksnelheid. Dat laatste wordt
nu met behulp van de uitdrukking rot v gedaan. In de handboeken wordt beweerd: rot v = 2ω.
We gaan dat controleren.
We gaan terug naar een stroming in het horizontale vlak. Zoals we hebben
gezien, geldt voor de z–component van de rotatie:
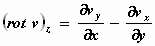
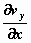 geeft aan hoe snel de snelheidscomponent in de y–richting in grootte
verandert als je langs de x–richting varieert. Evenzo geeft
geeft aan hoe snel de snelheidscomponent in de y–richting in grootte
verandert als je langs de x–richting varieert. Evenzo geeft 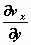 aan hoe snel de x–component van de snelheid in grootte varieert langs
de y–richting. Dat lijkt weinig met een hoeksnelheid ω
te maken te hebben, maar we zullen het zien.
aan hoe snel de x–component van de snelheid in grootte varieert langs
de y–richting. Dat lijkt weinig met een hoeksnelheid ω
te maken te hebben, maar we zullen het zien.
 |
Vraag:
Als voor de stroming in de binnenbocht van een rivier geldt vx
= 0,1 . y m/s (tot het midden van de rivier) en vy = –
0,0002. x2 m/s (tot 150 m verderop in de
x-richting), bereken dan de rotatie op
een punt 10 m vanaf de oever en 50 m verderop, dus x = 50 m,
met de formule voor
de z-component van rot v |
Voorbeeld
We bekijken een model van een orkaan (hurricane, cycloon).
In het centrum van het oog (met straal R) van de orkaan is het
windstil, maar naarmate je dichter bij de rand van het oog komt, waait het
steeds harder. Precies op de rand is de windsnelheid het grootst en naarmate je
nog verder verwijderd raakt van het oog neemt de wind weer af. De wind draait
cirkels zodat de richting altijd loodrecht op de straal naar het centrum van het
oog staat (zie fig. 4a). Het model bestaat uit het volgende:
vanaf het centrum tot de rand van het oog is de grootte van de
windsnelheid evenredig met de afstand r tot het centrum, dus v
= c . r. Dit wordt rotatiestroming genoemd. De rotatie
van een gewoon wiel gedraagt zich net zo.
vanaf de rand van het oog neemt de grootte van de snelheid omgekeerd
evenredig met de afstand r tot het centrum af, dus v= k/r.
Dit wordt circulatiestroming genoemd
op de rand van het oog r = R voldoet de snelheid aan beide
vergelijkingen, zodat daar geldt c.R = k/R. (zie fig 4b)
Met zo'n model kan je berekeningen doen en de uitkomsten vergelijken met een
werkelijke orkaan.
Gezien de verhalen van de "gelukkigen" die door het oog van de
orkaan zijn gekropen en die de complete rust aldaar prijzen, zal dit model
voor het ooggedeelte niet goed kloppen.
(Zie ook via het KNMI de websites over orkanen)

Figuur 4a Het windveld in en rond het oog van een orkaan
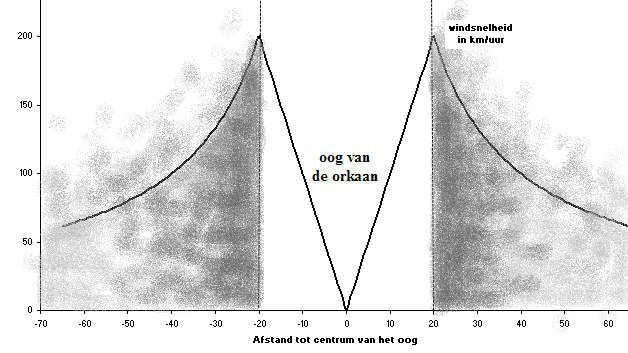
Figuur 4b Model van de windsnelheden
We gaan rot v berekenen in het "ooggebied" en
daarbuiten. We maken gebruik van de definitie van een cirkel waarbij we de
oorsprong van het assenstelsel in het centrum van het oog plaatsen: r2
= x2 + y2
Voor de rotatiestroming in het centrale deel krijg je dan: 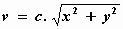 en
en
voor de circulatiestroming buiten het centrale
deel: 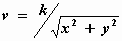
Met behulp van tekening 5 kunnen we de x–component en de y–component
bepalen.
Voor de rotatiestroming krijg je
vx = – v . sin φ = – c .
r . sin φ = – 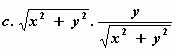 = – c . y
en
= – c . y
en
vy = + v . cos φ =
– c . r . cos φ = + 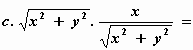 + c . x
+ c . x
Dus: vx = – c . y
en
vy = + c . x
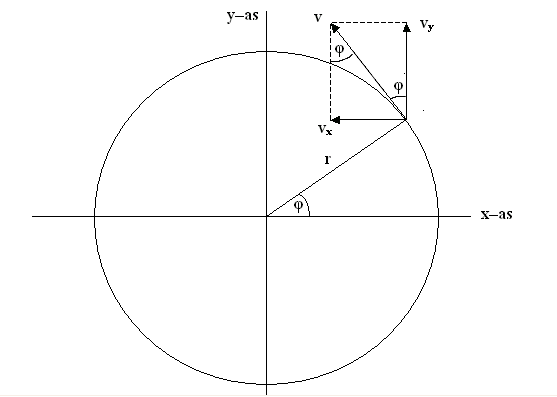
Figuur 5 De componenten van de snelheid bij een cirkelvormige
beweging
Deze eenvoudige formules voor vx en vy
zijn gemakkelijk te differentiëren. Let op: om rot v te bepalen, pas je
partiële differentiatie toe, dus als je naar x differentieert, beschouw y
als constante en omgekeerd.
We krijgen dan: 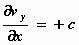 en
en 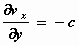 . .
Hiermee
wordt:
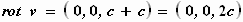
 | Wat betekent dit? |
In de eerste plaats is de rotatie voor het type rotatiestroming een
constante, overal in het gebied waar de rotatiestroming optreedt, in het oog van
de orkaan, heeft hij dezelfde waarde. Dus "het’ roteert binnen het oog
overal in dezelfde mate. Dat klopt wel, want als je twee punten A en B
bekijkt, zijn die ten opzichte van elkaar na één rondje ook een rondje ten
opzichte van elkaar gedraaid (zie fig. 6). Het punt B bevindt zich
eerst rechts van het punt A en een halve ronde later bevindt B
zich links van het punt A. Dat geldt voor alle punten, of je ze nou ver
uit elkaar kiest of vlak bij elkaar.
 |
Welke betekenis heeft hier de constante c in de formule v = c . r
? |
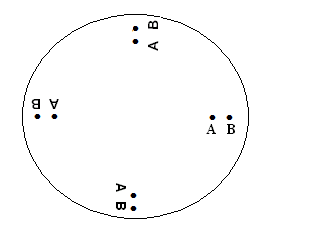
Figuur 6 Rotatiestroming
Neem eens c = 2 π, dan is v
= 2 π . r, dat wil zeggen dat de
snelheid van een punt dat zich op een afstand r van het middelpunt van de
cirkel bevindt zodanig is dat per seconde één rondje wordt afgelegd. De hoek φ
(zie fig. 4) die de voerstraal tussen het middelpunt en het bewegende punt met
de x–as maakt, is dan na één seconde 360º of 2π
radialen groter geworden. Diezelfde 2π!
Als we de hoek in radialen uitdrukken, is c dus de hoeksnelheid ω
(= de
toename van de hoek per seconde) in radialen per seconde.
De waarde 2c van de z–component van rot v is dus
gelijk aan tweemaal de hoeksnelheid. Je vraagt je af wat de wetenschappers heeft
bezield om af te spreken die factor twee in te voeren. Waarom niet gewoon rot v gelijk
te stellen aan de hoeksnelheid ω?
Dat zou veel eenvoudiger zijn.
Om achter deze raadselachtige afspraak te komen, bekijken we ook de
circulatiestroming (zie fig. 7) waarvoor, zoals we zagen, de volgende
snelheid geldt:
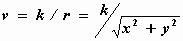
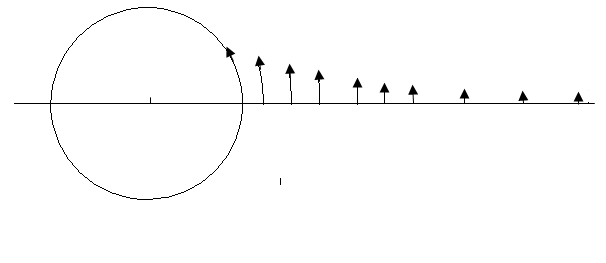
Figuur 7 Circulatiestroming
Hierbij is
vx = – v. sin φ = – 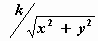 . .
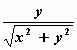 = = 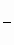 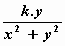 en
en
vy = v . cos φ = 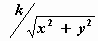 .
. 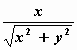 = + = + 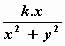
Nu bepalen we rot v met 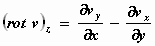
We hoeven alleen maar de z–component te bepalen omdat de rotatie in
het xy–vlak plaatsvindt. Dan heeft de rotatievector, zoals eerder is
gezegd, slechts een component in de z–richting.
We bepalen de afgeleiden met de quotiëntregel voor differentiëren :
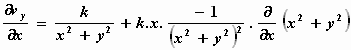 =
= 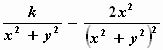 .k .k
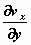 geeft op analoge wijze
geeft op analoge wijze 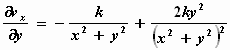
Neem nu 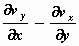 en het resultaat komt uit op nul!
en het resultaat komt uit op nul!
Terug
Dat is heel gek, ronddraaiende vloeistof die geen rotatie bezit. Dat verwacht
je niet.
Daarmee komen we op de essentie van het begrip rotatie. Als de rotatie in het
xy–vlak plaatsvindt, wordt de rotatie gevonden door de hoeksnelheid
langs de x–as en die langs de y–as bij elkaar op te
tellen. Die hoeksnelheden hoeven namelijk niet gelijk aan elkaar te zijn
en door ze op te tellen, krijg je een maat voor de rotatie van het gehele
elementje.
Deel het nog even door twee, zou ik zeggen, dan heb je de gemiddelde
hoeksnelheid als maat voor de rotatie, dat is toch wel zo
aardig! Eigenwijs, dat doen "ze"
niet.
Maar, hoor ik je sputteren, je moet ze niet optellen, maar van elkaar
aftrekken.
Dat is een interessante kwestie. In de volgende figuur 8a is een
elementje getekend dat een kleine rotatie tegen de wijzers van de klok in heeft
ondergaan als gevolg van de snelheden waaraan het is
blootgesteld. Eerst
vielen twee loodrecht op elkaar staande lijntjes van het elementje samen met de x–as
en de y–as en na korte tijd maakten ze daar een hoek mee. Het lijntje
waar vy bij staat, laat de verplaatsingen zien in de y–richting
. De hoekverdraaiing die het lijntje ondergaat, vind je met de afgeleide
van vy naar x (=de richtingscoëfficiënt). In de
tekening is het een positieve hoek en 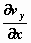 is
ook positief. is
ook positief.
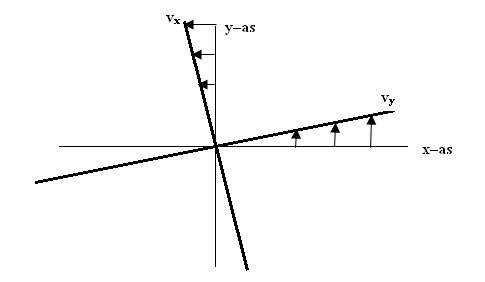
Figuur 8a De hoekverdraaiing langs de twee assen
Langs de y–as heeft het lijntje óók een positieve hoek afgelegd. Het
lijntje vx geeft de grootte van de snelheid in x–richting
weer. Maar in dit geval heeft 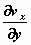 een
negatieve waarde, want met toenemende y wordt vx steeds
negatiever, hij wordt groter, maar in de negatieve richting.
Daarom
heeft een
negatieve waarde, want met toenemende y wordt vx steeds
negatiever, hij wordt groter, maar in de negatieve richting.
Daarom
heeft 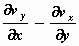 de betekenis van het bepalen van netto hoekverdraaiing voor
het elementje waarbij een hoek tegen de wijzers van de klok in
als positief wordt gerekend.
de betekenis van het bepalen van netto hoekverdraaiing voor
het elementje waarbij een hoek tegen de wijzers van de klok in
als positief wordt gerekend.
Voor de circulatiestroming is nu te begrijpen dat je op nul uitkomt: een
verticaal lijntje krijgt na korte tijd een positieve hoekverdraaiing (tegen de
klok in) en een horizontaal lijntje krijgt een even grote, negatieve verdraaiing (zie fig.
8b)
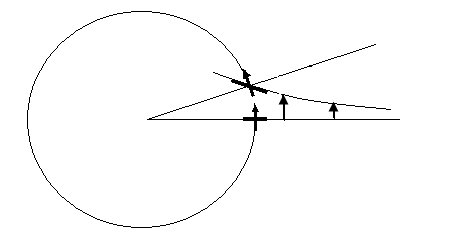
Figuur 8b Hoekverdraaiing bij circulatiestroming
De uitdrukking rot v geeft dus de som van de twee hoeksnelheden langs
de x–as en de y–as als ze allebei in de
zelfde richting draaien en dat is tweemaal de gemiddelde
hoeksnelheid van het elementje dat in de stroming mee dobbert.
Vandaar misschien de factor 2.
We kunnen het ook op de volgende manier bezien (zie fig. 9).
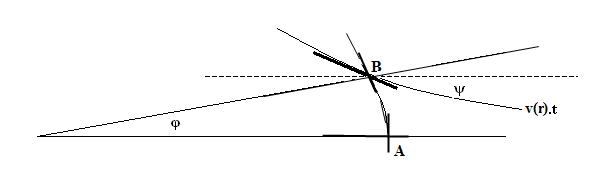
Figuur 9 Rotatie als gemiddelde van de hoeksnelheid van
horizontale en verticale assen van een elementje
Een elementje in de stroming stroomt van A naar B. Het gaat om
een cirkelvormige beweging. De hoek φ
is in radialen uitgedrukt: φ = v(r). t / r
dat wil zeggen: de snelheid ter plekke is v(r) en na t seconde is
de afgelegde afstand v(r) . t.
De hoek in radialen vind je door de
afstand te delen door de straal.
De stroming staat altijd loodrecht op de straal, dus een verticaal lijntje
bij A is bij B over dezelfde hoek φ
tegen de wijzers van de klok in afgebogen.
De hoeksnelheid ωvert
van een oorspronkelijk bij A verticaal gedeelte van het elementje, dat in t seconde over een hoek φ
is gedraaid, vind je door de hoek te delen door de tijd:
ωvert = v(r) /
r.
Een horizontaal lijnstuk bij A buigt juist met de wijzers van de klok
mee bij B. Voor een korte tijd t, als het lijnstuk zich nog
nauwelijks heeft verplaatst, mag je de beweging omhoog als rechtlijnig
beschouwen. De snelheid is wel afhankelijk van de afstand. De
lijn waar v(r).t bijstaat is de plaats waar de elementjes die zich eerst
op de x–as bevonden, zich na t sec bevinden. De afgeleide van v(r).t
naar r geeft op dat moment de richtingscoëfficiënt (tg ψ)
aan van de functie v(r).t (zie fig. 8). Nu geldt voor kleine hoeken tg
ψ = ψ en daarom kunnen we, als
we t klein houden, schrijven:
ψ = 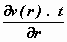 . .
Daaruit volgt voor de horizontale hoeksnelheid via delen door de tijd t:
ω hor = 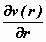
De gemiddelde hoeksnelheid over de verticale en de horizontale assen van het
elementje is
ω gemiddeld = ½ .(ωvert
+ ωhor) = ½ .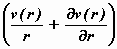
en dus is rot v = 2 ωgemiddeld
= ωvert + ωhor
.
Met de hier gegeven relaties kan de rotatie en de hoeksnelheid van stromingen
die een cirkel beschrijven, worden berekend (zie tabel 1). In deze tabel
zie je de rotatiestroming terug en ook de circulatiestroming.
Verder
staan onderaan de tabel twee buitenbeentjes: de
planetenbeweging en (nieuw) de cirkelrotatie stroming
van de planeten die te maken heeft met de
relativistische periheliumverschuivingen van hun
banen. De snelheid van deze twee bevat een halftallige exponent bij de afstand in tegenstelling tot de andere
stromingen in de tabel.
Toegevoegd is als "nieuw": de hadj-stroming, een bijzonder voorbeeld van een
cirkelvormige stroming (bestaande uit mensen) met een overal constante snelheid
. De hadj-stroming is de massastroom in Mekka van gelovigen
in de grote moskee rond het heiligdom Ka’aba, het rechthoekige, met
zwart doek omhulde bouwwerk op het centrum van het plein in de tempel.
Deze gelovigen lopen met een constante snelheid zevenmaal rond de Ka’
aba , tegen de wijzers van de klok in: v(r) = constant. De stroming
heeft een positieve hoeksnelheid en daarom ook een positieve rotatie,
die groter wordt naarmate de mensen dichter bij het heiligdom komen.
Ook hardlopers op een atletiekbaan die met
dezelfde snelheid in hun eigen baan door een
bocht lopen, vertonen ook dit type
rotatiestroming.
(We zoeken een tijdopname die de stroming goed weergeeft)
De rotatie en de hoeksnelheid van de circulatiestroming is, zoals we al
hadden berekend, gelijk aan nul. Je ziet dat die nul precies past in het rijtje
waarden in de derde kolom.
Tabel 1 Rotatie en hoeksnelheid van stromingen die een cirkel beschrijven
|
type stroming |
snel--
heid |
rotatie |
hoek t.o.v. de y–as |
hoek t.o.v. de x–as |
som van de hoeken |
hoek-
snelheid |
| |
v(r) |
rot v |
φ |
ψ |
φ + ψ |
ω |
| |
c.r4 |
5c.r3 |
c.r3.t |
4c.r3.t |
5c.r3.t |
2½ . c r3 |
| cirkelrotatie
van Ehrenfest schijf |
c.r3 |
4c.r2 |
c.r2.t |
3c.r2.t |
4c.r2.t |
2. c r2 |
| |
c.r2 |
3c.r |
c.r.t |
2c.r.t |
3c.r.t |
1½ . c r |
|
rotatiestroming |
c.r |
2c |
c.t |
c.t |
2c.t |
c |
|
hadj-stroming |
c |
c /r |
c.t / r |
0 |
c.t / r |
½ . c / r |
|
circulatie-
stroming |
c / r |
0 |
c.t / r2 |
–c.t / r2 |
0 |
0 |
| |
c / r2 |
–c / r3 |
c.t / r3 |
– 2c.t / r3 |
–c.t / r3 |
– ½ . c /r3 |
| |
c / r3 |
–2c / r4 |
c.t / r4 |
–3c.t / r4 |
–2c.t / r4 |
–c / r4 |
| |
c / r4 |
–3c / r5 |
c.t / r5 |
–4c.t / r5 |
–3c.t / r5 |
–1½.c / r5 |
| planetenbeweging |
c / r1/2 |
½ c / r3/2 |
c.t / r3/2 |
– ½.c.t /r 3/2 |
½.c.t /r 3/2 |
1/4.c.t /r 3/2 |
cirkelrotatie-stroming
van planeten (zie Artefact) |
c / r3/2 |
-½ c/ r5/2 |
|
|
|
|
We gaan nog een stap verder.
Wanneer we de integraal van de snelheid nemen langs een gesloten weg (de
kringintegraal) is de uitkomst meestal ongelijk aan nul. Bijvoorbeeld in figuur
10 . Wanneer je het vet getekende pad volgt en ieder stukje weg
vermenigvuldigt met de daar geldende snelheid dan heb je de integraal.
Neem aan dat de snelheid afhankelijk is van de afstand r tot het
centrum volgens v(r) = c .r (rotatiestroming). De integraal wordt
dan φ . r1 . c . r1
– φ . r2 . c . r2
= φ . c . (r12
– r22).
 |
De integratie langs de lijnen die naar het middelpunt gericht zijn, is nul omdat
de snelheid daar loodrecht op de weg staat. In dat geval is er geen component langs het
integratiepad en is de bijdrage nul. |
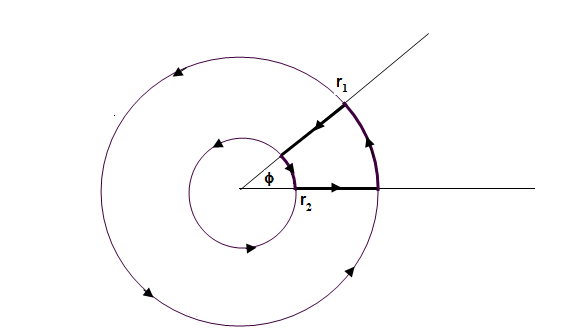
Figuur 10 Kringintegraal bij cirkelvormige stroming
Maar nu de circulatiestroming. Voor circulatiestroming geldt v(r) = c/r. De booglengte is evenredig
met r en de snelheid is omgekeerd evenredig met r. Daardoor vallen
de twee integraties langs de bogen tegen elkaar weg en de kringintegraal langs
het gesloten pad is nul. Ook op deze manier bekeken is de circulatiestroming een
uitzondering. De rotatie is nul en de kringintegraal is nul.
En toch draait hij!
Betekenis:
Dat de kringintegraal hier nul is, heeft nog een andere fysische betekenis.
Langs het integratiepad gaande, vermenigvuldig je namelijk de snelheid van de
water– of luchtstroom met de lengte van deze massastroom. De lengte is
evenredig met de massa die zich in dat deel van de cirkelboog bevindt. Het
product van massa en snelheid wordt de impuls genoemd. Voor een
snelheidsveld betekent dit dat de impuls in de buitenste cirkel even groot is
als de impuls in de binnenste cirkel. Dus, in het algemeen, iedere cirkel bevat
evenveel impuls.
Het wordt nog gekker als je weet dat er een verband is tussen de genoemde
kringintegraal en de rotatie van v . Volgens de stelling van Stokes
geldt:
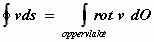
De kringintegraal van v langs s is gelijk aan de
oppervlakte-integraal van rot v over het oppervlak dat binnen het pad s
ligt. Als rot v = 0 , zoals bij de circulatiestroming, is de
oppervlakte-integraal gelijk aan nul en moet de kringintegraal dus ook gelijk
aan nul worden.
Voor één bijzonder punt geldt dit echter niet: het middelpunt van de
cirkel. Daar is rot v niet gedefinieerd (de afgeleide rent naar oneindig
naarmate je dit punt dichter nadert).
Als je de kringintegraal nu zo neemt dat het pad het middelpunt omsluit, krijgt
de integraal ineens een waarde. De snelheid keert niet om op enig deel van het
pad. Neem voor de lengte van de weg een cirkel met straal r : dus 2πr
. De snelheid is daar c / r. Dan heeft de kringintegraal de waarde: 2πr.c/r
= 2π.c. Dit is onafhankelijk van r, dus deze integraal
heeft altijd dezelfde waarde als hij het middelpunt omsluit. De constante c
is hier niet de hoeksnelheid (want die is nul) zoals bij de
rotatiestroming. De waarde 2π.c
wordt de wervelsterkte Γ (=
hoofdletter gamma) genoemd. Wegens het belang van de circulatiestroming wordt de
constante met k aangegeven, zoals we al deden bij de beschrijving van de
orkaan, en er geldt: Γ = 2πk,
waarbij k een maat is voor de snelheid van de circulatiestroming.
Dit
type stroming, de circulatiestroming, doet zich buiten wervelwinden en
draaikolken ook voor rond voorwerpen die door de lucht bewegen, van
tennisballen en vogels tot vliegtuigen, en daarmee kan het "effect"
van een draaiende bal tot en met de "lift" van een vliegtuig worden
verklaard.
Nog wat napraten:
De orkaan
De hoogste windsnelheden worden net buiten het oog gemeten, op 15 km van
het middelpunt, bijvoorbeeld 216 km/uur (= 60 m/s). We zitten dan in het gebied
van de circulatiestroming. v = k/15000 m/s, dus k = 15000 x v = 15000
x 60 = 900 x 10 3 m2/s
Dan geldt voor de wervelsterkte van deze orkaan: Γ
= 2 π x 900.103 = 5,65.106 m2/s
De draaikolk
Ook een draaikolk gedraagt zich min of meer als een circulatiestroming.
Prachtige, grote draaikolken zijn te bewonderen bij de getijdencentrale in Rance
tussen Normandië en Bretagne in Frankrijk (zie fig. 11). Bij elke
turbine, waar het water uit het bekken terugstroomt naar zee, ontstaat een draaikolk met een diameter van 5 tot 10 m voor het actieve
deel (Daarin spelen vissen van ongeveer 1 meter lengte). Als we de draaikolk van figuur
12 nader beschouwen, dan is de straal tot het gebied waar het wateroppervlak
weer praktisch horizontaal is, ongeveer 5 m. De snelheid waarmee het water op
die afstand ronddraait, is ongeveer: 3 m/s. Met v = k / r of 3 = k / 5,
vinden we k = 15 m2/s. De wervelsterkte van zo’n waterkolk
is dan ongeveer: Γ = 2π.k = 94,
pakweg 100 m2/s. Dat is een factor 104 tot 105
kleiner dan de kolk van de orkaan van hierboven.

Figuur 11 Draaikolken bij de getijdencentrale in Frankrijk
(Foto hjdorrestijn)

Figuur 12 Draaikolk van dichtbij (van links tot rechts ongeveer 4 m
)
(Foto h.j.dorrestijn)
Vlakke platen
Nog een leuk voorbeeld over rotatie in een stromende vloeistof. We bewegen
twee vlakke platen met een laagje vloeistof er tussen langzaam horizontaal over
elkaar. We doen het langzaam om turbulentie in de vloeistof te vermijden,
turbulentie die samenhangt met de viscositeit van de vloeistof, onderwerpen waar
we ons nu vooral niet in gaan verdiepen.
De onderste plaat ligt stil en de vloeistof die in direct contact staat met
de plaat heeft een snelheid nul. De bovenste plaat op een afstand z =
h van de onderste, beweegt met een snelheid vplaat en
de vloeistof die in direct contact staat met de bovenste plaat heeft ook die snelheid vplaat. We nemen aan dat de snelheid van de vloeistof
lineair verloopt tussen de onderste plaat en de bovenste plaat .
Je hebt dus een gelijkmatig verlopende snelheid van nul tot vplaat.
In formule: vx = 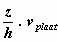
Er is niets dat lijkt te wijzen op rotatie, en toch blijkt er rotatie in te
zitten. Niet in het horizontale lijntje van een vloeistofelementje (zie fig.
13), dat verplaatst zich zonder draaiing, maar het verticale lijntje: dat
draait! Overal waar je een vloeistofelementje in gedachten neemt, zal het
verticale lijntje met de klok meedraaien: dat is een negatieve hoekverdraaiing.
We kunnen eenvoudig uitrekenen hoe groot de hoekverdraaiing na één seconde
(= de hoeksnelheid) is voor het verticale lijntje. In één seconde verplaatst de
bovenste plaat zich over een afstand vplaat meter. De
vloeistof bij de bovenste plaat heeft zich dan over dezelfde afstand verplaatst,
terwijl de vloeistof bij de onderste plaat, net als de onderste plaat zelf, zich
geheel niet heeft verplaatst. De hoek tussen de schuin lopende lijn en de
verticale lijn is de hoekverdraaiing in één seconde.
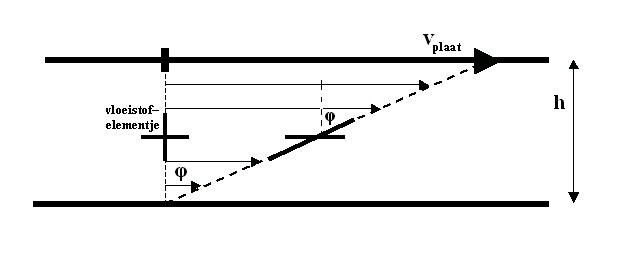
Figuur 13 Rotatie tussen twee onderling verschuivende vlakke platen
De hoek φ vinden we met tg
φ = – vplaat /
h.
De hoek φ(t) na t
seconde is te vinden met tg φ(t) = – vplaat.t/h.
De hoek φ(t) die hieruit volgt,
de inverse tangensfunctie, is een ingewikkelde functie, maar als we de
hoeksnelheid op een bepaald moment willen weten, kunnen we net zo goed twee kort
opeenvolgende momenten kiezen. Dan is φ(t)
een zeer kleine hoek en er geldt dan bij benadering: tg φ(t)
= φ(t). Als we de hoeksnelheid (= de hoek per seconde) willen
weten, nemen we de limiet voor t naar nul van φ(t)/t
.De hoeksnelheid wordt
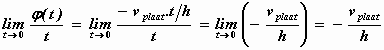
Je ziet dat de hoeksnelheid niet meer van t afhangt, op een afstand h
van de stilstaande plaat is de hoeksnelheid (en ook de rotatie) steeds
gelijk.
De hoeksnelheid van het vloeistofelementje wordt, zoals we bij de
cirkelvormige stromingen hebben gezien, de gemiddelde waarde van de
hoeksnelheden van de horizontale en de verticale as van het element:
ω = ½ .{0 + (–vplaat/h)}
= – ½ .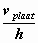
De rotatieas ligt in dit geval langs de y–as, in het horizontale
vlak en loodrecht op de x–as. De rotatievector wijst, wegens de
kurkentrekkerregel, van ons af naar de negatieve y–as.
We controleren de uitkomst van de hoeksnelheid met de formule voor rot v.
We behoeven alleen maar de y–component te berekenen omdat de
verandering van de snelheid langs de x–as uitsluitend in de z–richting
plaatsvindt:
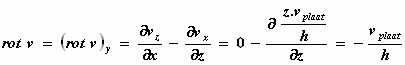
Het klopt met rot v = 2.ω
Je begrijpt dat met toenemende snelheid van de platen ten opzichte van elkaar
het feit dat de vloeistof rotatie bezit aanleiding zal geven tot kleine wervels
in de vloeistof waardoor de stroming op zeker moment turbulent zal worden.
Terug
Naar Uitleg §7 Sterren
|
|