Massa is een vorm van energie:

Naar Tweelingparadox 
Naar Uitleg § 10 Massa en snelheid 
Naar Uitleg Inhoud 
Naar  Vertaling E=mc2
Naar  Centrale Hal    

Einstein zal zich voor zijn kop hebben geslagen. Zijn artikel over de elektrodynamica van bewegende voorwerpen was de deur nog niet uit of hij ontdekte dat hij een uiterst belangrijke conclusie uit de theorie over het hoofd had gezien. Eind juni was zijn artikel door de uitgever ontvangen en het verscheen op 28 september in het tijdschrift "Annalen der Physik"( zie biografie). Maar op 27 september had de uitgever al de aanvulling ontvangen waarin de beroemde formule E = m . c² wordt afgeleid.

"Pffff, net op tijd!" zal hij hebben gedacht, want voor je het weet, leest iemand het die  vervolgens aan de haal gaat met de belangrijkste gevolgtrekking uit het artikel.

Hij gaf een titel aan de aanvulling in de vorm van een vraag: "Is de trage massa van een voorwerp afhankelijk van zijn energie–inhoud?"

"Nee!" was men geneigd te denken.

"Ja!" toont Einstein aan in drie A4-tjes.

Men wist wel dat de massa van een elektron toenam bij toenemende snelheid. Zoals we in §10 hebben gezien, sprak men over de longitudinale en de transversale massa van het elektron en Einstein toont daar al aan dat de massatoename ook voor materiële deeltjes moet gelden. Het verschijnsel werd door zijn vakbroeders nog gezien als een snelheidseffect op de elektromagnetische massa en alleen Einstein was tot het inzicht gekomen dat het een snelheidseffect was op elke vorm van trage massa. Maar dat de massatoename evenredig was met de energietoename, zoals Einstein hier aantoont, was volstrekt nieuw. Zijn bewijsvoering is vernuftig;  er is geen speld tussen te krijgen.

We volgen de eigenwijze jongeling:

Hij gaat even terug naar het voorgaande artikel "Over de elektrodynamica van bewegende voorwerpen" en meldt in een voetnoot dat de constante lichtsnelheid c in de Maxwell–vergelijkingen is ingebakken. Dat moet wel, want anders zouden ze niet onder de Lorentztransformatie dezelfde natuurwet opleveren. Toch doet Einstein zichzelf hier tekort, want het is juist zijn verdienste om voor de lichtsnelheid in het stelsel–in–beweging zowel als in het stelsel–in–rust dezelfde waarde c te nemen, terwijl Lorentz hardnekkig twee verschillende waarden toepaste. Alleen door de lichtsnelheid constant te nemen, blijken de Maxwellvergelijkingen in beide stelsels dezelfde vorm aan te nemen en daarmee te voldoen aan het relativiteitsprincipe. Dit betekent dat de Maxwellvergelijkingen de toets van de Lorentztransformatie doorstonden in tegenstelling tot de wetten van de mechanica, te beginnen met de wet van Newton F = m.a.

Vervolgens memoreert hij dat in §8 op basis van de Maxwellvergelijkingen en de uitdrukking  voor de energie van een hoeveelheid vlakke lichtgolven in de lege ruimte 

E = A²/ 8 π,

de volgende vergelijking was afgeleid voor de energie E in het stelsel-in-rust en de energie E' in het stelsel-in-beweging van die hoeveelheid licht

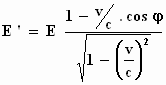
 (= stralingsenergie in het bewegende stelsel waarbij c negatief is genomen )

Het relativiteitsprincipe formuleert hij vervolgens nog een keer:

In deze versie heeft hij het woord "evenwijdige" toegevoegd om kromlijnige bewegingen, zoals rotaties, uit te sluiten.

De bovengenoemde formule gebruikt hij opnieuw, maar de energie E van de lichthoeveelheid geeft hij – in het origineel –aan met de kleine letter ℓ om de algemene formule aan te geven en vervolgens met de hoofdletter L als het specifiek gaat om de lichthoeveelheid die in zijn voorbeeld door een voorwerp wordt uitgezonden.

Hij bekijkt nu een voorwerp dat naar links en naar rechts in tegenovergestelde richting eenzelfde hoeveelheid lichtenergie L /2 uitzendt. Het licht mag onder een hoek φ ten opzichte van de x–as worden uitgezonden.

Als het voorwerp stilstaat verliest het dus een hoeveelheid energie L / 2 + L / 2 = L.

Wanneer dit voorwerp oorspronkelijk een hoeveelheid energie E₀ heeft, zal het na het uitzenden van het licht een hoeveelheid energie E₁ bezitten, waarbij de relatie geldt:

E₀ = E₁ + L

Dus  geldt:    E₀ – E₁ = L

Wanneer ditzelfde voorwerp zich nu ten opzichte van ons verplaatst met een snelheid v dan verplaatsen wij ons ten opzichte van het voorwerp met een snelheid – v .  De energiehoeveelheden van de bundels zullen veranderen volgens de formule voor E' die hierboven als "stralingsenergie in het bewegende stelsel" is aangehaald.

In het stelsel–in–beweging geldt ook de wet van behoud van energie, het energieprincipe. Als we de energie in het stelsel–in–beweging aangeven met accenten zal gelden:

E'₀ = E'₁ + L'  of    E'₀ – E'₁ = L'

Hierin is L' de gezamenlijke energie van de twee lichtbundels die in tegengestelde richtingen zijn uitgezonden. Voor L' mogen we met de formule voor "stralingsenergie in het bewegende stelsel" schrijven:

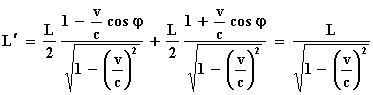
We zien hieruit dat L' groter is dan L. De energie van de lichthoeveelheid die in dezelfde richting beweegt als wij, neemt af en de energiehoeveelheid die ons tegemoet komt, neemt toe, maar de som van de toe– en afname is groter dan nul. 

Je kan dit zien als een gevolg van de verminderde hoeveelheid tijd waarin de bundels  in het bewegende stelsel worden uitgezonden, waardoor de frequenties van de lichtbundels gemiddeld moeten  toenemen.

Vervolgens pakt Einstein dit gedachte-experiment met de hem kenmerkende zorgvuldigheid aan. Hij vergelijkt de energiehoeveelheid van het voorwerp in het stelsel–in–beweging E' met de energiehoeveelheid in het stelsel–in–rust E . Het verschil E'–E is de kinetische energie van het voorwerp, die we aangeven met de hoofdletter K.

Het verschil E'₀ – E₀ is de kinetische energie K₀ vóór het uitzenden en het verschil E₁'– E₁ is de kinetische energie K₁ ná het uitzenden van de lichthoeveelheden.

Maar, wijst Einstein er dan op, de energie van het voorwerp is op een willekeurige additieve constante na bepaald. Additief betekent dat deze constante er naar believen bij kan worden opgeteld. Hij zal de potentiële energie in gedachten hebben gehad die op een constante na is bepaald. Het nulniveau van de potentiële energie moet worden afgesproken. 

In het stelsel–in–rust kiest men bijvoorbeeld voor die constante de waarde A en in het stelsel–in–beweging kiest men B. Het verschil B – A = C . 
Dan is E'₀ – E₀ = K₀ + C en E₁'– E₁ = K₁ + C, want, zegt Einstein, C verandert niet ten gevolge van het uitzenden van licht door het voorwerp. Het voorwerp verplaatst zich niet op dat ene moment. 
Daarom valt C er uit en hoeven we er geen aandacht aan te besteden.

Nog voor een normaal mens een probleem ziet, heeft Einstein al aangetoond dat het geen probleem is!

We krijgen dan voor de kinetische energie:
Voor het uitzenden van het licht: E'₀ – E₀ = K₀, dit is de energie van het bewegende object min de energie van het rustende object voordat het licht wordt uitgezonden.

Na het uitzenden van het licht: E'₁ – E₁ = K₁

De verandering van de kinetische energie wordt dus
K₀ – K₁ = (E '₀ – E₀ ) – (E ₁' – E₁ ) = (E'₀ – E'₁ ) – (E₀ – E₁), dit is de energieverandering van het 
bewegende object min de energieverandering van het rustende object.  

We hebben een bladzijde terug gezien dat (E₀ – E₁) = L en dat (E'₀ – E'₁ ) = L'
Hiermee krijgen we K₀ – K₁ = E'₀ - E₀ - E'₁ + E₁= = L'– L, zodat gebruikmakend van de uitdrukking voor L':

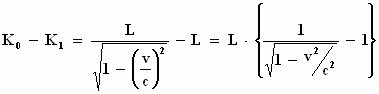
 Om de uitdrukking te vereenvoudigen, gebruikt Einstein een benadering via de eerste twee termen van een reeks die we al eerder hebben gezien (§4 blz. 904 Vertaling en in de Uitleg halverwege). Hij schrijft:        
                    

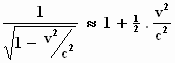
We zullen ter verduidelijking deze Taylor–reeks uitbreiden tot 4 termen:

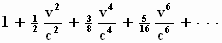
Daarmee wordt het verschil in kinetische energie:

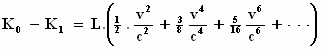
De snelheid v van het bewegende stelsel, van waaruit wij het voorwerp waarnemen, is voor en na het uitzenden van het licht gelijk gebleven. Als er dus een verschil in de kinetische energie  
 ½ m v² voor en na het uitzenden van het licht is , kan dat alleen maar tot uitdrukking komen via de massa, omdat v onveranderlijk is. We moeten schrijven:

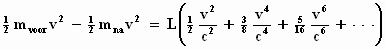
Alle termen delen door ½ v² geeft :    

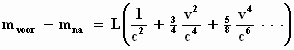
Conclusie: door het uitzenden van de hoeveelheid lichtenergie L is de massa bij benadering afgenomen met L/c² als je alleen de eerste term van de reeks meerekent (de volgende termen zijn naar verhouding enorm klein voor "gewone" snelheden v ).

Als je de limiet neemt voor v gaat naar 0, dan gaan de termen met de machten van v ook naar 0, dus voor een stilstaand voorwerp geldt exact:

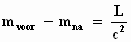
Dus de afname van de massa heeft niets te maken met stilstand of beweging van het voorwerp!!

Einstein knoopt hier direct de veralgemenisering aan vast dat het voor het voorwerp niet uitmaakt in welke energiesoort het zijn energie is kwijt geraakt. In zijn voorbeeld gaat het om elektromagnetische straling, maar het voorwerp kan zijn energie ook verliezen via warmtegeleiding of door uitzetting (een gas) of via een elektrisch veld of wat niet al, zodat verlies van iedere vorm van energie voor een voorwerp verlies van massa betekent. Omgekeerd: als je, op welke manier dan ook,  energie toevoert aan een voorwerp neemt de massa van het voorwerp toe.

Ter verduidelijking berekent Einstein nog dat als de energie van een voorwerp met L  "groter wordt, de massa met L / 9.10²⁰ gram groter wordt (of als L kleiner wordt, wordt de massa zoveel kleiner). Hij drukt de energie L uit in "erg", een toentertijd gangbare energie-eenheid die je krijgt met als eenheid van lengte de centimeter en als eenheid van massa de gram (tijd in seconde).

Met de nu gebruikelijke eenheden: lengte in meter, massa in kilogram en de tijd in seconde, komt het er op neer dat als we een hoeveelheid energie van E joule aan een voorwerp toevoegen, zijn massa toeneemt met m = E/c² = E / 9.10¹⁶ kg.

In dit stadium wijst Einstein er al op dat radioactieve stoffen de eerst aangewezen stoffen zijn om de relatie tussen energie en massa aan te tonen, nog niet bevroedend dat uiteindelijk het overdonderende bewijs via de atoombom zou worden geleverd.
Hij komt tot de fysisch en filosofisch misschien wel minstens zo interessante slotsom dat via straling massa wordt overgedragen van het ene voorwerp op het andere.

Tot zover het artikel.

We komen nog even terug op de kinetische energie van een voorwerp:
Wanneer de energie E die aan een stilstaand voorwerp wordt toegevoerd in bewegingsenergie van het voorwerp wordt omgezet, is de energie van het voorwerp toegenomen en zal de massa m van het voorwerp moeten toenemen volgens:

Hierin is m_o de rustmassa, dat wil zeggen: de massa van het niet-bewegende voorwerp.

De kinetische energie van het bewegende voorwerp is dus m.c² – m_o. c²_.

In §10, blz.920 heeft Einstein al aangetoond dat de bewegingsenergie E die een voorwerp krijgt dat door een kracht in een zekere richting wordt versneld, de waarde aanneemt:

E = m_o. c² (γ–1)

Gelijkstellen geeft: m_o. c² (γ–1) = m.c² – m_o. c²

Hieruit volgt: m = γ. m_o.

Voor de kinetische energie van het voorwerp mogen we dus schrijven: E = (γ–1).m_o.c².

Dat is wel wat anders dan het vertrouwde ½ .m_o v². Het moet echter wel iets met elkaar te maken hebben. De link tussen beide uitdrukkingen wordt duidelijk als je, zoals we iets terug ook hebben gedaan, voor γ schrijft: 
                γ = 1+ ½ .v²/c² + …..

Als v klein is t.o.v.  c zijn de overige termen te verwaarlozen.

Dus γ - 1 = ½ .v²/c² + …..
Hiermee wordt  m = γ. m_o= (1+ ½ .v²/c² ). m_o=  m_o+½ .v²/c² . m_o
De massa is van het voorwerp met een rustmassa van m_o  is dus met ½ .v²/c² . m_o  kg toegenomen

Terug